2 展開の原理

基本はユークリッド幾何学である。内容例には「平行線は相交わらない」がある。ちなみに非ユークリッド幾何学では「平行線は無限遠点で交わる」であり、平行線も交わる線として包含する。実質的には同じことで、太陽は一点で、その光を放射しているが、その放射点より遠い地球上では、平行光と見做してよい。

2.1 空間の幾何

幾何というのはGeometry：土地測量法の意味のある外国語に対応する用語で、図形の科学であるが、現図に応用する方法は、本書では計算でなく作画で解く範囲に限られる。

作画である以上、図形を描く平面上に捉えなけばならない。この捉え方として、平行光による投影を用いる。太陽光による影をイメージするとよい。

一般に空間図形の科学は「図学」として体系化されており、造船特有でない部分はそれを参照すれば足りるので、本編では取挙げない。

現在普及を進めている数値現図では、方法は計算であり、実長と実名は方向を持つ量であるベクトルとし、空間は空間のまま取扱える。本編で説明している作画現図の対比として、付記しておく。

2.2 空間から平面へ

形状を表わす要素は線なので、空間にある線を平面に投影する様子を考える。

太陽光は真上から降り注ぐ。線と見做す棒は地面に対して斜めに宙に浮いているとする。真下に棒の影ができる。影の長さは棒より短い（図2.2.1）。展開するとは、平面上に実長で形状を描くことだから、この棒＝線の実長を影の形から求めねばならない。

造船現図では、これを次のように考える。

?@線の下端点を含み、地面に平行な平面を想定する。この平面への影の長さは、先に見た図2.2.1と変らない。

線の上端点も掴まえないと、実長は決まらないから、この上端点を含む、やはり地面に平行な平面を想定する（図2.2.2）。

?A次に、この線とその影を含む平面を、更に付加えて想定する（図2.2.3）。この面は太陽光に平行（図2.2.1参照）だから、前の?@で想定した二つの平面とは直交する。

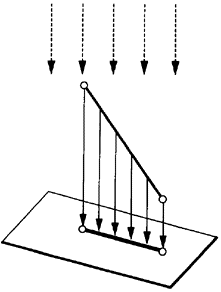
図2.2.1

前ページ　　　目次へ　　　次ページ